超详细 ｜ 灰狼优化算法原理及其实现(Matlab)_1

由于元启发式算法的灵活性，推导自由，简单，许多作者相继提出新的元启发式算法。这些算法正在迅速成为解决复杂优化问题的重要工具。最流行的元启发式算法有以下四种类型，

第一种是进化算法：其中比较有代表性的有遗传算法(GA)和差分进化算法(DE);

第二种是仿自然的优化算法，包括万有引力搜索算法(GSA)和中心引力优化算法(CFO)来模拟自然物理规则；

第三种是仿人类的优化算法，例如免疫算法(IA)和思维进化算法(MEA)；

第四种是群体智能（SI）算法，包括粒子群优化算法(PSO)、蚁狮算法（ACO）等；

大多数关于元启发式算法的研究都集中在探索和开发上。SI算法的一些特征不同于其他三类算法，有时可以在这两个阶段获得更好的结果。与其他三种类型的元启发式算法相比，SI算法在搜索过程中保留解空间的信息，并能够记忆最佳解。此外，更少的参数和操作能够便于理解和控制SI。SI是集体的智力行为。因此，群体中的个体间的协作能帮助种群避免陷入局部最优。

随着SI算法的发展，Mirjalili等[1]于2014年提出了一种新型SI算法：灰狼优化算法(Grey Wolf Optimization,GWO)。GWO通过模拟灰狼群体捕食行为，基于狼群群体协作的机制来达到优化的目的，这一机制在平衡探索和开发方面取得了不错的效果，并且在收敛速度和求解精度上都有良好的性能，目前已广泛应用于工程领域，如：神经网络、调度、控制、电力系统等。本文将对其原理进行介绍并通过MATLAB实现

1 灰狼优化算法原理
2 代码目录
3 算法性能
4 源码获取
5 总结

GWO算法模拟自然界中灰狼种群等级机制和捕猎行为。通过4种类型的灰狼(𝛼，𝛽，𝛿，𝜔)来模拟社会等级，通过狼群跟踪﹑包围、追捕、攻击猎物等过程来模拟狼的捕猎行为,实现优化搜索目的。GWO算法具有原理简单、并行性﹑易于实现,需调整的参数少且不需要问题的梯度信息,有较强的全局搜索能力等特点。

在函数优化方面, Mirjalili等通过对29个基准函数的测试表明,GWO算法在求解精度和收敛性方面明显优于粒子群优化(PSO)、重力搜索算法(GSA),差分进化(DE),进化规划(EP)和进化策略(ES)的结果。

在GWO算法中, 首先是在搜索空间中随机产生灰狼族群，为构建灰狼的社会等级制度模型,将种群中适应度值最优的解、次优的解和第三优的解分别看作α狼、β狼和𝛿狼,而剩余的解被视为𝜔狼。然后由α狼、β狼和𝛿狼来负责引导, 𝜔狼则跟随着α狼、β狼和𝛿狼,通过搜寻猎物﹑包围猎物和攻击猎物来完成狩猎优化，最终获取最优解。

1.1 社会等级

设计GWO算法时,狼群中每一个灰狼代表了种群的一个潜在解,为了描述灰狼的社会等级﹐将α狼的位置视为最优解﹔将β和𝛿狼的位置分别作为优解和次优解; 𝜔狼的位置作为其余的候选解。在GWO算法中,由a , β和𝛿引导搜索(优化),而𝜔狼跟随前面3种狼。

1.2 包围猎物

捕猎过程中，灰狼群体会先包围猎物，该行为的数学模型可以表示为: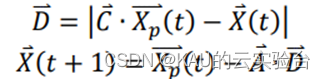

其中，𝑡代表当前迭代的次数，𝑋𝑝 (𝑡)为第𝑡次迭代中猎物的位置向量，𝑋 (𝑡)为第𝑡次迭代中灰狼的位置向量。𝐴和𝐶为协同向量，计算方式为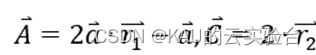

其中𝑎中的分量在迭代过程中从2到0线性递减，𝑟?1 和𝑟?2 为[0,1]中的随机向量

1.3 狩猎

灰狼有能力识别猎物的位置并包围它们。狩猎通常由α狼引导, β和𝛿也可能偶尔参与狩猎。然而,在一个抽象搜索空间中,灰狼并不知道最优解(猎物)的精确位置。为了模拟灰狼的狩猎行为,假设α(最优候选解)、β和𝛿拥有更多关于猎物潜在位置的知识。因此,在每次迭代过程中,保存迄今为止获得的3个最优解,迫使其他狼(包括𝜔)根据最优搜索的位置采用以下公式更新它们的位置: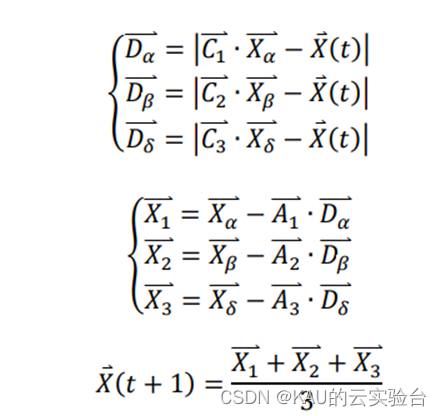

其中𝑋𝛼?，𝑋𝛽?，𝑋𝛿?代表当前迭代中𝛼，𝛽，𝛿的位置向量，𝑋 (𝑡)为第𝑡次迭代中个体的位 置向量，𝐶1 ?，𝐶2 ?，𝐶3 ?为随机向量，𝐷𝛼?，𝐷𝛽?， 𝐷𝛿?代表群体中其他个体与𝛼，𝛽，𝛿之间的距离，𝑋 (𝑡 + 1)为个体更新后的位置向量。

下图给出𝜔狼或其他狼(候选狼)如何根据二维搜索空间中的𝛼，𝛽，𝛿狼来更新其位置。从中可以看出,最终位置将在搜索空间中由𝛼，𝛽，𝛿狼的位置定义的圆内的随机位置。换句话说, 𝛼，𝛽，𝛿狼估计猎物的位置,其他狼围绕猎物随机更新它们的位置。

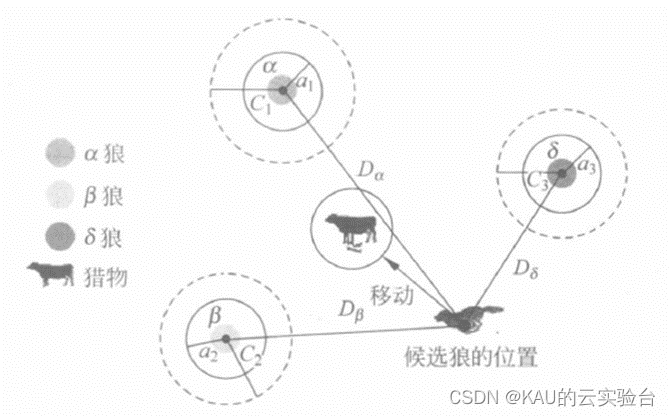
图源于智能优化计算与涌现计算

1.4 攻击猎物

灰狼在猎物停止移动时通过攻击猎物来完成捕猎。攻击猎物确定猎物位置，即得到最优解， 这一过程主要通过迭代过程中收敛因子𝑎从 2 到 0 的递减来实现，于是群体在迭代结束后，获取最优解。

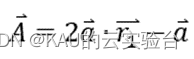
在 GWO 算法中，通过 a 值逐渐线性减少，使得 A的波动范围也随之线性减少，从而模拟狼群逼近猎物的行为。C 是［0，2］之间随机值，C表示狼所在位置对猎物影响的随机权重，由于C值是一个随机值，用于防止算法寻优时无法摆脱局部最优，对搜寻全局最优解发挥了非常重要的作用，增强了算法的全局搜索能力、鲁棒性与收敛性。

1.5 优化过程

GWO 算法优化流程为首先创建一个灰狼种群， 然后在迭代过程中将最优的三个解定义为 α、β 和 δ，而后其他个体根据 α、β 和 δ 的位置判断猎物所在位置，从而更新自己的位置。GWO 算法的流程如图所示

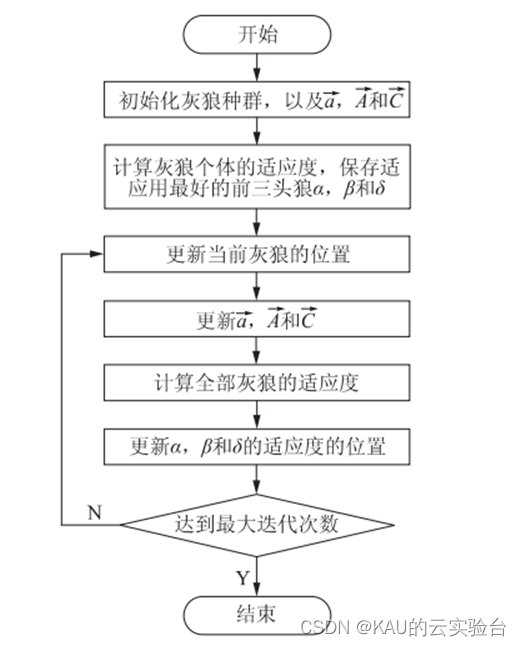
代码注释完整，其中部分GWO程序如下：

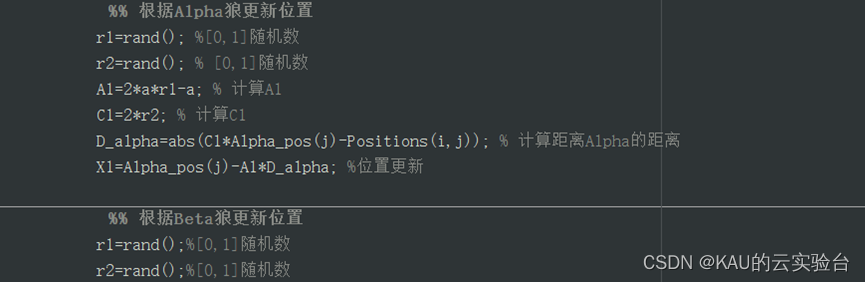
代码获取方式见文末

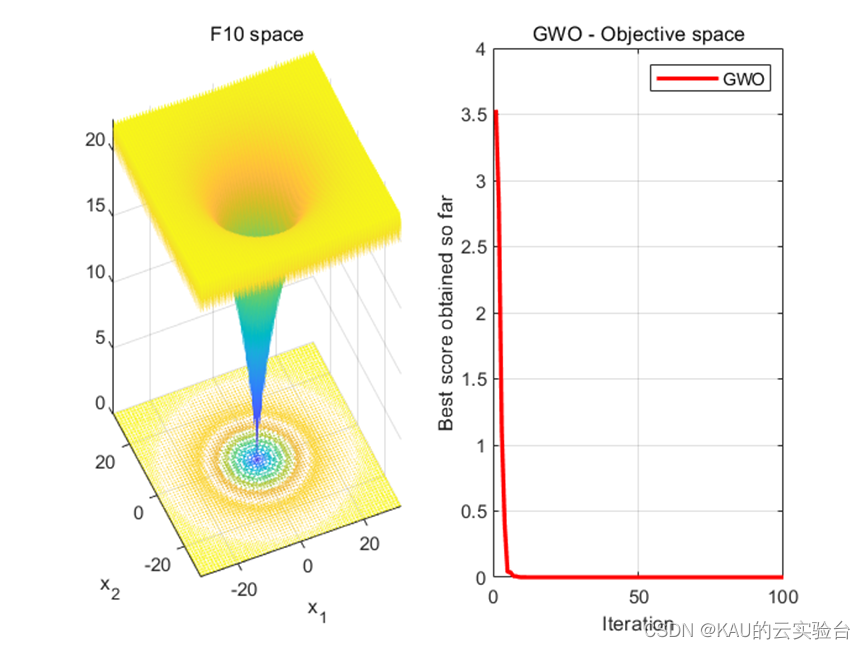
采用CEC的测试函数F10来初步检验其寻优性能，F10的数学表达式如下：

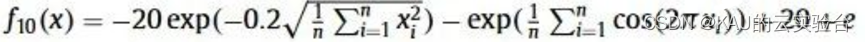
运行GWO.m，结果如下

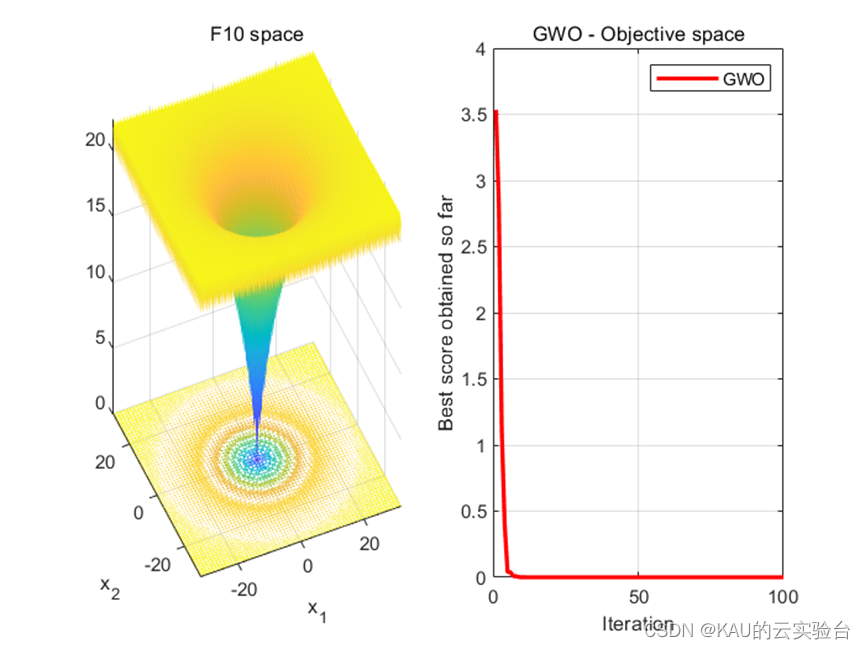
尽管GWO有良好的性能，并在处理工程问题方面相当的成功，但与传统的元启发式方法一样，仍有需要改进的地方。当应用于解决多模态问题时，GWO的性能会下降。许多文献中已经提出其改进策略，如：改进控制参数，GWO的a参数控制其探索和开发的过程，其随迭代过程发生线性变化，但线性函数不能很好的应用于多模态问题，因此可以尝试对其进行非线性的改进，其次还可以尝试完善其位置更新机制，引入随机行走等方法来更新狼的位置以解决其局部停滞和过早收敛的问题等等。

作者也将在后面的文章中更新对于灰狼算法的改进，欢迎关注~

[1]MIRJALILI S,MIRJALILI S M,LEWIS A.Grey Wolf Optimi-zer[J].Advances in Engineering Software,2014,69(3):46-61.

灰狼优化算法MATLAB源码获取：

公众号：KAU的云实验台 回复 GWO

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞(?_)?(不点也行)